Planck konstanten

Formål:
Øvelsens formål er at bestemme Plancks konstant
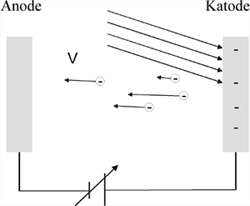 Apparatur Apparatur
- Fotocelle
- Hg-lampe
- Spejlgalvanometer
- Batteri
- Spændingsdeler
Teori:
Figuren til højre illustrerer princippet bag øvelsen:En fotocelles katode bestråles med lys med bølgelængden l. Herved emitteres der fotoelektroner fra katoden. Fotoeletronerne bevæger sig over imod anoden. Dette er fotostrømmen. Imellem katoden og anode lægges der en modspænding. Ved at variere modspændingen varieres størrelsen af fotostrømmen.Kendes l kan man ud fra ændringen af fotostrømmen som funktion af modspændingen beregne Plancks konstant: h.
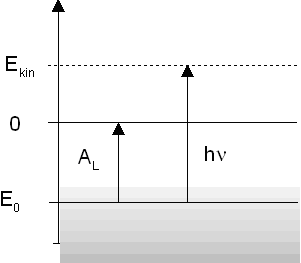 På figuren til højre er vist et energiniveaudiagram fotoelektronerne.Energien E0 er den maksimale energi elektronerne kan have i metallet - hvis temperaturen er 0 K. På grund af termiske exitationer vil nogle elektroner have en energi, som er lidt højere. (Angivet med skygge). Løsrives en elektron med energien E0 af en foton med energien h·n vil elektronen have en kinetisk energi givet ved: På figuren til højre er vist et energiniveaudiagram fotoelektronerne.Energien E0 er den maksimale energi elektronerne kan have i metallet - hvis temperaturen er 0 K. På grund af termiske exitationer vil nogle elektroner have en energi, som er lidt højere. (Angivet med skygge). Løsrives en elektron med energien E0 af en foton med energien h·n vil elektronen have en kinetisk energi givet ved:
hvor AL er løsrivelsesarbejdet.
Fotoelektronernes kinetiske energi findes ved at bestemme den modspænding Ustop, der netop skal til for at opbremse fotoelektronen:
og Einsteins fotoelektriske ligning lyder derfor:
Denne ligning viser, at afbildes e · Ustop som funktion af n fås en ret linie med hældning på h og skæring med y aksen lig løsrivelsesarbejdet AL.
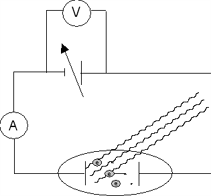 Udførelse: Udførelse:
Kredsløbet vist til venstre opbygges. Som lyskilde bruges en Hg-lampe.Sæt et filter ind imellem Hg-lampe og fotocelle. Noter bølgelængden af det lys passerer igennem filteret og rammer fotocellen.Varier modspændingen og mål de tilhørende strømstyrker.I skal have mange punkter for små modspændinger (<0,5 V)
Databehandling:
For hver bølgelængde gøres følgende:Korriger for evt. negative strømstyrker ved at fratrække alle måleresultater den mindste strømstyrke: Herved bliver alle strømstyrker ikke negative.
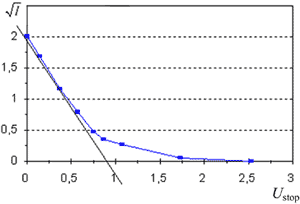 Afbild derefter Afbild derefter 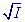 som funktion af Umodspænding. For små Umodspænding kan man vise, at målepunkterne skal ligge på en ret linie, hvis skæring med U-aksen er Ustop. Herefter tegnes en graf med e · Ustop som funktion af n. Find h ud fra denne graf. som funktion af Umodspænding. For små Umodspænding kan man vise, at målepunkterne skal ligge på en ret linie, hvis skæring med U-aksen er Ustop. Herefter tegnes en graf med e · Ustop som funktion af n. Find h ud fra denne graf.
|