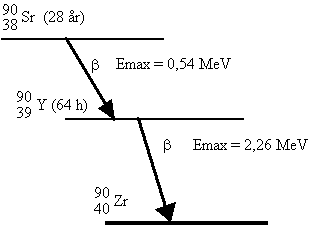
Forsøg med radioaktivitet

Bestemmelse af halveringstid

Øvelsens formål

Formålet er at bestemme halveringstiden og henfaldskonstanten for henfaldet af en eksiteret bariumisotop.

Forsøgsopstilling

Minigeneratoren er en radioaktiv kilde, der indeholder den langtlevende cæsiumisotop med halveringstiden T_½ = 27 år. Henfaldsdiagrammet er vist nedenfor. Det ses, at ¹³7Cs for 92%'s vedkommende henfalder til en eksiteret bariumkerne, 137Ba. Denne metastabile kerne henfalder, med kort halveringstid, under g-udsendelse til den stabile . Det er g -strålingen fra dette sidste henfald vi registrerer med Geiger-Müller røret.

Henfaldsdiagram:

Forsøgets udførelse

MINIGENRATOREN malkes for ved at presse ca. 5 ml elueringsvæske (0,04 M HCl i 1% NaCl) gennem MINIGENERATOREN. Eluatet opsamles i et lille bægerglas.

Forsøgsopstilling

GM-røret opspændes lodret lige over væsken. GM-tælleren (med serielt interface) forbindes til pc'en. I programmet Datalyse vælges den pågældende tæller, dernæst vælges »Counting, Thalve«. Måletiden indstilles til 10 sekunder.

Sæt tælleren igang før MINIGENERATOREN malkes, så målingerne kan starte straks efter malkningen. Der tælles i 5 til 6 minutter. Herefter fjernes reagensglasset og indholdet smides i vasken. Er det forsvarligt!?

Mål herefter baggrundsstrålingen, f.eks. i 10 minutter og omregn til pr 10 s.

Baggrundstrålingen kan fratrækkes som søjleopration i tabellen i Datalyse.

Bemærk, at første måling fra 0 s til 10 s afbildes til tiden t₁ = 5 sekunder, osv...

Rapporten skal indeholde:

De korrigerede tælletal er proportionale med væskens aktivitet. Kun en del af g -strålerne fra væsken rammer GM-røret, og GM-rørets effektivitet over for g-stråling er kun ca. 1%.

Afbild de korrigerede tælletal som funktion af tiden t og vælg logaritmisk 2.akser. Ud fra formlen for aktiviteten A = A₀·e^-kt forventes en ret linie. Bestem halveringstiden T_½ vha. grafen. (benyt lineær regression).

Udregn herefter henfaldskonstanten k.

Den semilogaritmiske afbildning bliver ikke en perfekt ret linie. Hvorfor ikke?

Lav en skitse af GM-rørets indre og forklar hvordan det registrerer g-stråling.

Beregn g-strålingens bølgelængde og frekvens.

Tabelværdien for halveringstiden er T_½ = 156 s.

Gammastrålers absorption i bly

Når g-stråler passerer et stof, svækkes strålingen pga. fotoelektrisk effekt, comptoneffekt og måske pardannelse. For at halvere strålingens intensitet skal den passere gennem adskillige cm aluminium eller flere mm bly. Ved gennemgangen svækkes strålingens intensitet eksponentielt med tykkelsen x af det passerede stof:

I = I₀·e-mx,

hvor I₀ er den usvækkede strålings intensitet og svækkelseskonstanten m afhænger af stoffets Z-værdi og af g-strålingens bølgelængde (energi).

Forsøgsopstilling

Opspænd GM-røret og g-kilden, således at afstanden fra kilde til rør er ca 10 cm. Mellem røret og kilden anbringes 2 mm tykke Pb-plader. Bestem absorptionslagets tykkelse x (brug skydelære) og strålingens intensitet I (korrigeret for baggrundsstråling, som du har målt i forsøg med halveringstid). Målingerne foretages vha. programmet Datalyse. Samme opstilling som i foregående forsøg. Her vælges blot »Counting (xhalve)« i menuen.

Tabellen kan se ud som ovenfor. Du fratrækker baggrundstrålingen som en søjleoperation. Dernæst vælger du Funktioner, Graf i tabellen og tegner en graf over korrigerede tælletal som funktion af tykkelsen.

Rapporten skal indeholde:

Afbild I_korr som funktion af x på semilogaritmisk papir. Tegn den bedste rette linie og bestem halveringstykkelsen x_½.

Beregn absorptionskoefficienten m =

Find vha. en graf for absorptionskoefficient som funktion af Energien af g-strålingen i Datahåndbogen ud af, hvilken svækkelsesform der er den væsentligste for g-strålingen. g -strålingens energi er E = 0,66 MeV.

Middelværdi og spredning for tælletal - poissonfordelingen

Øvelsens formål

Formålet er at bestemme middelværdi og spredning for tælletal fra et Geiger-Müller-rør, der måler på en radioaktiv kilde med (næsten) konstant strålings-aktivitet (der er tale om g -henfald af den eksiterede Ba-137*. Halveringstiden for kilden er 30.1 år. Der tælles i et stort antal tidsperioder af samme længde.

Desuden skal den målte fordeling af tælletal sammenlignes med den tilsvarende Poissonfordeling (med samme middelværdi som de målte tælletal) - se senere!

Opstilling:

Forsøgsopstilling

Forsøgets udførelse:

g-kilden anbringes i kildeholderen (se opstilling). GM-røret anbringes så nogle cm fra kilden, se figuren.

På pc'en vælges programmet Datalyse. I programmet indstilles G-M tælleren til at tælle i en passende valgt tidsperiode. Vælg 1 sekund, ellers bliver du ikke færdig i timen. Du skal måle i lang tid! Hvor længe kan du jo overveje mens du måler.

Efter hver tidsperiode sender tælleren tallet til pc'en, nulstilles og tæller videre.

På pc'en optælles hyppighederne for de indkommende tælletal - og samtidig tegne stolpediagrammet med hyppighederne på skærmen.

Udskriv grafen og en tabel med tælletal og hyppigheder. Bemærk, at Datalyse beregner middelværdi og spredning for de målte data. (se dem i memoen).

Rapporten skal indeholde:

Besvar følgende spørgsmål (vis ved beregninger i rapporten)

1. Hvor mange % af perioderne har talletal i intervallet [m-s, m+s] ?
2. Hvor mange % af perioderne har talletal i intervallet [m-2s, m+2s] ?

Desuden skal du beregne kvadratroden af middelværdien m og sammenligne denne med spredningen s. Kan du på denne baggrund acceptere følgende postulat:

»Spredningen på tælletal er ca. kvadratroden af (middelværdien af) tælletallet«

Poisson-fordelingen

Poisson-fordelingen med middelværdi m er givet ved følgende sandsynligheder:

P(X = k) =

hvor X er den stokastiske variabel, der som værdimængde har tælletallene 0,1,2,...

Poissonfordelingen fremkommer som følge af, at de registrerede henfald forekommer på fuldstændig tilfældige tidspunkter. Dette er igen en følge af, at det er umuligt at forudsige, hvornår den enkelte atomkerne vil henfalde: hver atomkerne har en bestemt henfaldssandsynlighed pr tidsenhed, og denne er uafhængig af, hvor »gammel« atomkernen er. Der er altså tale om en ægte stokastisk proces!

Poisson-fordelingen kan fås som grænseværdi af Binomialfordelingen b(n,p), hvor middelværdien m = n·p fastholdes under grænseovergangen n gående mod uendelig. Spørg eventuelt din matematiklærer!

Note om »Skolekilderne«

De tre radioaktive kilder er fremstillet af Risø, og er beregnet til undervisningsbrug. Kilderne er ufarlige, men følgende sikkerhedsregler skal overholdes:

1 Kilderne holdes mindst 25 cm fra kroppen.

2 Kilderne må kun berøres på den halvdel af plexiglasholderen, der er længst væk fra metalbeholderen.

a-kilden: denne indeholder Americium-241. Americium forekommer ikke i naturen. Am-241 blev første gang fremstillet kunstigt i 1944 vha den store cyklotron i Berkley. Am-241 udsender a -partikler (5,5 MeV) og blød g-stråling (0,060 MeV). T_½ = 460 år.

a-henfald

b -henfald

b -kilden: denne indeholder strontium-90, der fremstilles i store mængder fra atomreaktorers brændselselementer. Sr-90 omdannes ved en b-udsendelse (Emax = 0,52 MeV) til yttrium-90, der ved en ny b -udsendelse omdannes til zirkonium-90. b-partiklerne fra yttrium har en maksimal energi på 2,26 MeV, og det er disse partikler, man måler, idet partiklerne fra strontium absorberes i plexiglasset. Halveringstiderne for de to henfald er henholdsvis 28 år og 64 timer.

g-kilden: denne indeholder caecium-137, der ligesom stontium-90 fremstilles ud fra atomreaktorers brændselselementer. Cs-137 udsender både b- og g-stråling, og kilden er derfor omgivet af et plexiglaslag, der absorberer b-strålingen. Halveringstiden er 27 år.

Se henfaldsdiagrammet i starten af vejledningen.