Luftmodstand

luftmo01.zip

Hvis man ser bort fra »meget store« hastigheder er luftmodstanden på et legeme i bevægelse stort set proportional med vf(v), hvor v er farten og f(v) er en funktion af v for hvilken det gælder, at 1 £ f(v) £ 2. For almindelig luft ved normalt tryk kan man vise ved forsøg, at f(v) kan sættes lig med 2, når

,

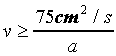hvor a er en karakteristisk størrelse for legemet (f.eks. kunne a være et kvadrats sidelængde eller en cirkels diameter). Hvis a er 8 cm fås v < 9 cm/s. Dette at f(v) kan sættes lig med 2 simplificerer udregningerne ganske meget.

Vi gør altså den tilnærmelse, at luftmodstanden er proportional med v², dvs. F_l = k·v². Proportionaliteskonstanten k er givet ved udtrykket k = 0,625 kg/m³·A·c_w, hvor A er legemets tværsnitsareal (set forfra under bevægelsen) og c_w er modstandskoefficienten Konstanten 0.625 kg/m³ afhænger i øvrigt af luftens massefylde og viskositet.

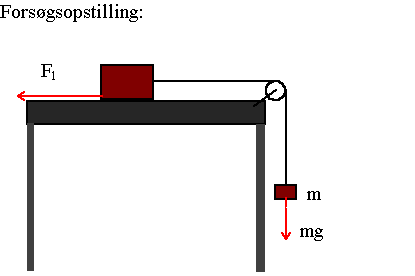
For et legeme, der på en luftpudebane drives af et træklod (ligesom i øvelsen Newtons 2. lov) fås:

F_res = mg - F_t = mg - kv² = (m+M)a

Vi har her set bort fra gnidning samt den lille luftmodstand på vognen og træklodet.

Da 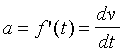fås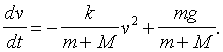

Dette kaldes en differentialligning. Den ubekendte størrelse er funktionen v(t). Da udregningerne er noget komplicerede, skal løsninghen gives her:

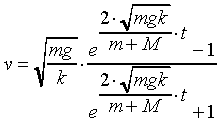
Prøv at kontrollere løsningen ved at differentiere v, og undersøg, om dette resultat stemmer med differentialligningen.

Det ses umiddelbart af udtrykket for v, at 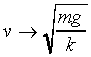for t ® ¥.

Da funktionen v(t) er lidt kompliceret, vil det være oplagt at bruge EDB, når man skal sammenligne den udregnede og den målte hastighed.

Den målte hastighed findes vha. samme opstilling som i øvelsen Newtons 2. lov Herefter kan den målte hastighed afbildes grafisk

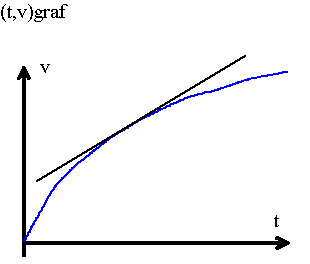
I et EDB-program kan man i det teoretiske udtryk for v indsætte forskellige værdier for c_w og derved prøve, om man kan få overensstemmelse med de målte værdier.

En anden måde at angribe problemet på kunne være at tegne tangenter til grafen for vmålt, og derved få bestemt (tangenthældningen).

Herefter udregnes F_l = mg - (m+M)a.

Dernæst kan man undersøge, om dette stemmer overens med udtrykket

F_l = 0.625 kg/m³·c_w·v².

En tredie måde kunne være at blæse ludt fra en støvsuger henimod måleobjektet, og måle luftstrømmens hastighed med en vindmåler. Kraften på måleobjektet kan måles med et dynamometer.

Prøv at eksperimentere med alle tre metoder, og undersøg om de giver samme resultat.