Det matematiske pendul

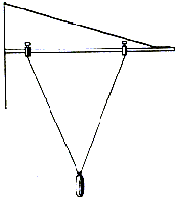
Som matematisk pendul benyttes et tungt lod ophængt i en sytråd. Pendulbevægelsen er en ujævn cirkelbevægelse, hvor radius (= pendullængden), med god tilnærmelse kan sættes lig den lodrette afstand fra ophængningspunktet til loddets tyngdepunkt. l) med Ophængningen er bifilar, som vist på figuren. Derved undgår man kegleformede svingninger.

Svingningstiden T er tiden for en hel periode. T bestemmes ved måling af tiden for et stort antal svingninger. Hvis svingningerne registreres med fotocelle og tæller, bør der tælles over 60 sekunder. Anvendes i stedet stopur og manuel optælling, registreres fx 40 svingninger. En periode kan regnes fra loddets passage af midterstillingpn til næste passage i samme retning.

Beskriv i rapporten den anvendte måleprocedure og tilrettelæg selv et sæt målinger til undersøgelse af de nedenfor nævnte 4 forhold:

• Undersøg med fast pendullængde om fx. de første 40 svingninger og de næste 40 svingninger tager samme tid. Før loddet ud fra ligevægtsstillingen og lad det svinge nogle gange før målingerne startes.
• Med samme pendullængde - men med to forskellige pendulmasser - måles svingningstiden.
• For fastholdt pendullængde og pendulmasse måles svingningstiden for pendulamplituder på fx 10°, 20°, 40° og 80°. Overvej, hvorledes man med en lineal kan måle sig frem til disse vinkler, når snorens længde er kendt.

I lærebøger kan du finde følgende formel for svingningstiden gældende for det matematiske pendul under forudsætning af små udsving:

Heraf ses, at T² og l må være proportionale. Tilrettelæg og gennemfør en eksperimentel undersøgelse af denne påstand (udfør målinger med mindst 6 forskellige pendullængder).

Alle måledata indføres i passende skemaer. Vælg en fornuftig databehandlingsmetode i hvert tilfælde. Husk konklusion til de enkelte undersøgelser.

Lav kritik af dine målinger.