Impulsbevarelse i det skrå stød

Øvelsens formål

Formålet er at eftervise, at den samlede bevægelsesmængde er bevaret i et stød.

Forsøgsopstilling

Apparatet er en krum skinne, som en kugle kan rulle nedad, således at den forlader skinnen med en vandret hastighed. For at denne hastighed skal kunne reproduceres, er skinnen foroven forsynet med en stopklods, så kuglen kan starte i samme højde hver gang. Ved skinnens nederste ende kan en anden kugle anbringes i en drejelig holder, således at kuglerne kan udføre et mere eller mindre skråt stød.

Forsøgets udførelse

Skinnen spændes fast i bordpladen, og på gulvet lægges papir. Punktet lodret under stødstedet afmærkes med en blyant og findes vha. en lodlinie i form af en tynd snor med et søm i enden. Dette punkt kaldes O.

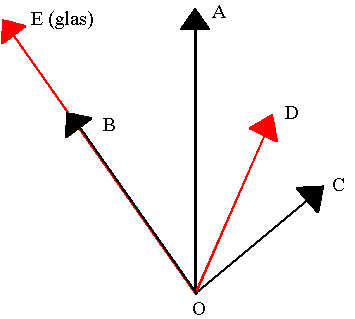
»nedslagsfigur«

Kuglernes nedslagspunkter synliggøres vha. karbonpapir. Først lader man en stålkugle gennemløbe skinnen uden efterfølgende stød. Dens nedslagspunkt markeres, efter at man har gennemført forsøget 10 gange. Kuglen slippes altid med en hurtig bevægelse. Punktet kaldes A.

Herefter laves 10 gange et forsøg, hvor kuglen støder mod en stålkugle magen til. De to nedslagspunkter kaldes B og C.

Til sidst laves 10 forsøg, hvor stålkuglen støder mod en glaskugle. Nedslagspunkterne kaldes D og E.

Teori

Kuglerne er under deres fald kun påvirket af tyngdekraften, og da deres udgangshastigheder er vandrette, rammer de gulvet samtidigt. Da kuglernes vandrette hastighedskomposanter er konstante, vil vektorerne OB, OC, OD og OE derfor repræsentere kuglernes hastigheder lige efter stødet. OA repræsenterer første kugles hastighed lige før stødet.

Impulsbevarelsen lyder

m₁v + 0 (hvilende kugle) = m₁u₁ + m₂u₂ ,

hvor v er kugle 1's hastighed før stødet og u₁ og u₂ er kuglernes hastigheder efter stødet.

Da kuglernes vandrette bevægelse er jævn: r = v·t, og t = , hvor h er O's højde over gulvet, gælder f.eks.:

OA = v·t = v·

Impulsen før stødet er altså m₁v =.

Opskriv et simpelt udtryk for impulsbevarelsen udtrykt ved »hastighedsvektorerne«, OB, OC, osv., når kuglerne er lige tunge.
Vis, at vinkel BOC = 90°, hvis stødet er elastisk.
Opskriv et udtryk for impulsbevarelsen - igen udtrykt ved »hastighedsvektorerne« - , når kuglerne ikke er lige tunge.
Vis herved, at DA = 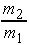·OE